Nein. Und warum das mit Nacho Analytics auch nicht geht, das erklärt Markus ganz wunderbar.
Tom Alby
art – Blog – Neue versus wiederkehrende benutzer ein nutzloser kpi

Ich habe den Sinn eines bestimmten Diagramms in Google Analytics nie verstanden, und zwar den des Tortendiagramms, das das Verhältnis der neuen Nutzer zu den wiederkehrenden Nutzern zeigt. Es war früher im Standard-Dashboard, das ein Nutzer nach dem Login sah, und ich hatte mich immer für dieses Diagramm entschuldigt, wenn ich während meiner Zeit bei Google eine Google Analytics-Demo gezeigt hatte.
Was ist so schlimm an diesem Diagramm? Zunächst einmal wird ein Tortendiagramm für statische Zusammenstellungen verwendet. Wenn ich wissen möchte, wie die Geschlechteraufteilung meines Kurses ist, dann ergibt ein Tortendiagramm Sinn. Die Geschlechter werden sich größtenteils nicht ändern während des Kurses.
Die meisten Webseiten wollen aber die Anzahl ihrer Besucher erhöhen, sei es durch neue Nutzer, wiederkehrende Nutzer oder beides. Eine Entwicklung ist also das Ziel, und somit ist ein Tortendiagramm nicht sinnvoll, da es ja statische Konstellationen zeigt. Ein Liniendiagramm, das die Entwicklung über die Zeit zeigt, ist in den meisten Fällen sicherlich eine bessere Wahl.
Ich gehe jetzt aber noch einen Schritt weiter und behaupte, dass diese beiden Metriken nichts miteinander zu tun haben und deswegen auch nie in einem Diagramm dargestellt werden sollten. Neue Benutzer können wiederkehrende Nutzer werden, müssen es aber nicht. Und wiederkehrende Nutzer können in dem gleichen Zeitraum auch neue Nutzer gewesen sein, sie werden dann zwei Mal gezählt. Wenn ein Nutzer also in beiden Teilen des Tortendiagramms auftauchen kann, was sagt das Verhältnis der beiden Teile zueinander dann aus?
Neue Nutzer entstehen durch Marketing. Idealerweise kommen wiederkehrende Nutzer dadurch zustande, dass die Inhalte so toll sind, dass die Nutzer nicht mehr ohne sie leben wollen. Wenn ich keine neuen Nutzer bekomme, dann muss ich mein Marketing optimieren. Wenn meine Nutzer nicht wiederkehren, dann muss ich meine Inhalte optimieren. Da wir immer auf der Jagd nach sogenannten “Actionable Insights” sind, warum sollten wir dann zwei Metriken in einem Diagramm darstellen, wenn sie unterschiedliche korrigierende Maßnahmen erfordern?
Außerdem: Ich kann zwei Wochen lang viel Geld für Marketing ausgeben, so dass sich der Anteil neuer Nutzer massiv erhöht und der Anteil wiederkehrender Nutzer in der Ratio dadurch stark verringert. Selbst wenn die absolute Zahl wiederkehrender Nutzer gleich bleibt, würde die Ratio uns vermitteln, dass wir weniger wiederkehrende Nutzer hätten. Aus diesem Grund sollten diese beiden Metriken nie zusammen als Ratio, sondern stets getrennt angezeigt werden. Serviervorschlag: Ein Graph mit der Entwicklung der neuen Nutzer mit den Akquisekanälen, ein Graph mit den wiederkehrenden Nutzern und den Inhalten, die für die Wiederkehr verantwortlich sein könnten.
Diese Frage stellte heute eine Kursteilnehmerin, und diese Frage finde ich aus mehreren Gründen gut. Wir wissen nicht, ob neue Nutzer wiederkehrende Nutzer sein werden (abgesehen von denjenigen neuen Nutzern, die in unserem Zeitraum neu als auch wiederkehrend sind, weil sie 2 Mal kamen, aber sie könnten sich natürlich in der Zukunft gegen einen weiteren Besuch entscheiden). Insofern könnte jeder Nutzer, der einmal dagewesen ist, irgendwann einmal in der Zukunft wiederkommen. Technisch gesehen kann kein Nutzer, der seine Cookies gelöscht hat, als wiederkehrender Nutzer bei uns wieder auftauchen, von User ID-Gebrauch einmal abgesehen. Aber dennoch finde ich die Frage spannend, da ich mich in einem anderen Kontext mit ihr beschäftigt habe: Ab wann muss ich einen Kunden bei einem Produkt, das regelmäßig gekauft wird, als verloren ansehen?
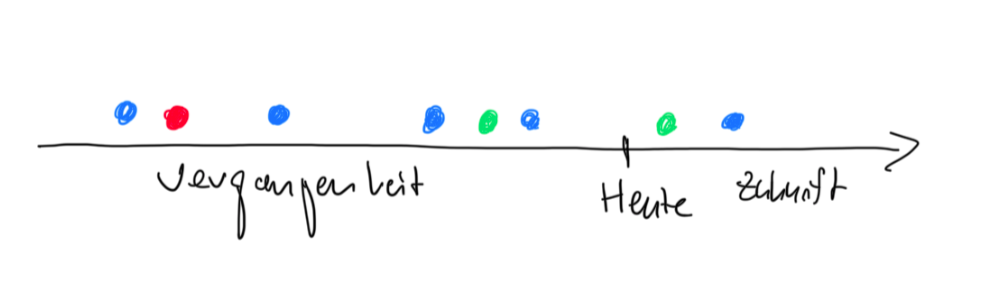
Die Grafik soll meine Gedanken dazu verdeutlichen. Wir haben einen Punkt “Heute” und drei Nutzer, blau, rot und grün. Nutzer blau kommt in mehr oder weniger regelmäßigen Abständen vorbei. Bei dem Zeitpunkt “Heute” würde ich davon ausgehen, dass er auch in Zukunft wiederkommt, zumindest scheint die Wahrscheinlichkeit hoch zu sein. Nutzer grün war erst vor kurzem da. Er hatte vielleicht keine Chance, wiederzukommen. Nutzer rot war vor langer Zeit da, und verglichen mit den Zeitabständen, die Nutzer blau zwischen seinen Käufen hat, scheint die Wahrscheinlichkeit einer Wiederkehr gering zu sein. Er kann wiederkommen, aber ihn würde ich eher mit einem Incentive anlocken als Nutzer grün, der eventuell eh wiederkommen wird (pull-forward cannibalization).
Wir können also nichts Genaues über nicht-wiederkehrende Nutzer sagen, denn wir kennen die Zukunft nicht. Aber wir können mit Wahrscheinlichkeiten rechnen. Bei reinen Nutzern eventuell nicht so spannend. Aber bei Shop-Kunden schon spannender.
Google Analytics kann mitunter fies sein, denn manche Dimensionen gepaart mit Segmenten verhalten sich nicht so, wie man das zunächst denken mag. Dank Michael Janssens und Maik Bruns‘ Kommentare auf meine Frage in der von Maik gegründeten Analyse-Gruppe kann ich heute beruhigt schlafen gehen und bin wieder ein bisschen schlauer geworden.
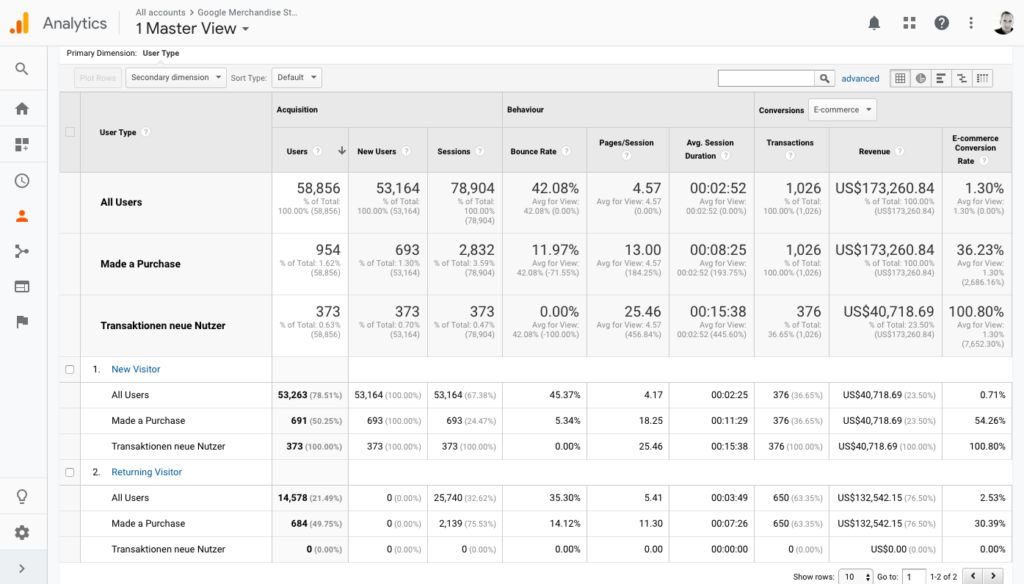
Die Frage kam heute im Analytics-Kurs auf: Wie kann es sein, dass ich mehr Neue Nutzer als Transaktionen habe, wenn ich in dem Segment “Hat einen Kauf getätigt” bin? Den Link zum Bericht gibt es hier, die Annahme, die ich hatte, war die: Wenn ich ein Segment von Nutzern habe, die einen Kauf getätigt haben, und dieses Segment im Bericht “Neue vs. wiederkehrende Nutzer” verwende, dann gehe ich davon aus, dass ich in dem Bereich Neue Besucher + Haben einen Kauf getätigt nur die Nutzer sehe, die in ihrem ersten Besuch etwas gekauft haben. Allerdings sehen wir hier in diesem Bericht 691 Nutzer, aber nur 376 Transaktionen. Wenn meine Erwartungshaltung stimmen würde, dann müsste die Zahl hier gleich sein. Ist sie aber nicht.
Wir sehen hier auch andere Widersprüche, und der Vollständigkeit halber fangen wir mit ihnen an. So liegt die Zahl der neuen Nutzer bei 53.263, die der wiederkehrenden Nutzer bei 14.578. Allerdings haben wir nur 58.856 Nutzer insgesamt, also weniger als die Summe der neuen und der wiederkehrenden Nutzer.
Diese Diskrepanz ist einfach erklärt: Wenn ein Nutzer innerhalb des Berichtszeitraums das erste Mal kommt, dann ist er ein Neuer Nutzer. Kommt er innerhalb des Berichtszeitraums ein zweites Mal, dann ist er auch ein Wiederkehrender Nutzer. Er wird also zwei Mal gezählt, einmal bei den Neuen Nutzern, einmal bei den Wiederkehrenden Nutzern. Bei “Alle Nutzer” wird er aber nur einmal gezählt.
Schauen wir einmal in die Spalte Transactions, so sehen wir, dass diese nicht mehrmals gezählt werden. Das ist logisch, denn sie können sich nur einmal als Transaktion definieren
Maik brachte noch den Punkt, dass globale Seiten etwas verzerrte Daten aufweisen, weil Google Analytics um Mitternacht alle Sessions neu startet, so dass ein neuer Besucher, der um 23:55 kommt und um 0:01 eine zweite Seite aufruft, an diesem zweiten Tag auch als Neuer Besucher gilt, wie am ersten Tag. Es ist derselbe Nutzer, aber er wird zwei Mal als neuer Nutzer gezählt (siehe Quelle hier). Aber kann das dazu führen, dass wir so viel mehr Neue Nutzer als Transaktionen haben? Sicherlich, der Google Merchandising Store ist globalgalaktisch aktiv, aber wird rund um die Uhr so viel gekauft?
Die Lösung (Danke, Michael!) liegt darin, dass das Segment “Made a Purchase” gepaart mit “Neuer Besucher” nicht mit einem UND verknüpft sind, d.h. wir können hier Nutzer drin haben, die irgendwann gekauft haben, aber nicht unbedingt im ersten Besuch. Das wird deutlich, wenn wir unsere beiden Segmente mit einem Segment vergleichen, das Michael gebaut hat:
Michaels Segment ist so gebaut, dass es die UND-Verknüpfung nutzt:

Wir haben hier Sessions, in denen ein Nutzer neu sein muss und gleichzeitig mindestens eine Transaktion. Und wir sehen plötzlich, dass wir für die 376 Transaktionen 373 Nutzer haben, d.h. es muss Nutzer gegeben haben, die in ihrem Besuch mehrere Transaktionen gehabt haben. Mit anderen Worten, die Neuen Besucher in unserem Segment “Made a Purchase” haben zwar alle einen Purchase gemacht, aber 691 minus 376 Transaktionen wurden von diesen Neuen Besuchern nicht während ihres ersten Besuchs gemacht, sondern in einem späteren. Die Verknüpfung des Berichts und des Segments könnte man so formulieren: Zeig mir alle Benutzer, die in irgendeiner Session eine Transaktion hatten und innerhalb des Berichtszeitraums auch ihren ersten Besuch.Sie bedeutet nicht, zeig mir alle Nutzer, die in ihrer ersten Session auch eine Transaktion haben.
In Zukunft werde ich etwas genauer schauen, wie die Verknüpfung eines Segments mit einem Bericht zu interpretieren habe. Denn das war, wie gesagt, etwas fies
Über Personas habe ich mich ja schon an anderer Stelle ausgelassen, in diesem Artikel geht es um die datengetriebene Generierung von Personas. Ich halte mich an die Definition des Persona-Erfinders Cooper und sehe eine Persona als Prototyp für eine Gruppe von Nutzern. Dies kann auch fürs Marketing interessant sein, denn schließlich lässt dich damit eine bedürfnis- und erfahrungsorientierte Kommunikation zum Beispiel auf einer Webseite erstellen. Personas sind keine Zielgruppen, aber dazu an anderer Stelle mehr.
Den perfekten allgemeingültigen Weg für datengetriebene Personas habe ich auch noch nicht gefunden. Externe Daten sind nicht für alle Themen vorhanden, der ursprüngliche Ansatz von 10-12 Interviews schwierig, und interne Daten haben den Nachteil, dass sie ja nur die Daten derjenigen beinhalten, die man schon kennt, nicht derjenigen, die man vielleicht noch erreichen möchte. Die Wahrheit liegt im Zusammenlegen verschiedener Datenquellen.
Webanalyse-Daten bieten einiges an Nutzungsverhalten, und je nachdem wie eine Seite aufgebaut ist (zum Beispiel ob sie schon auf die verschiedenen Bedürfnisse unterschiedlicher Personas ausgerichtet ist), lässt sich nachvollziehen, inwieweit sich die verschiedenen Nutzergruppen tatsächlich wie erwartet verhalten. Oder man versucht daten-getriebene Personas aus dem Nutzungsverhalten auf der Webseite zu generieren. Alles unter der Einschränkung, dass die Nutzer die Seite ja erst einmal finden müssen, es ist also nicht sicher, dass wirklich alle Personengruppen tatsächlich auf diese Seite zugreifen und deswegen wichtige Personas übersehen werden. In diesem Artikel geht es um einen Spezialfall dieser automatisierten Persona-Generierung aus Webanalyse-Daten, der aus algorithmischer Sicht und der dazugehörigen Visualisierung spannend ist. Über Erfolge berichtet bekanntlich jeder gerne, hier mal ein Fall, wo der Misserfolg zeigt, in welche Richtung weitere Arbeit gehen könnte.
Die Erfahrungen aus dem Web Mining werden nur selten mit Personas in Verbindung gebracht, obwohl schon vor mehr als 10 Jahren einiges an Forschung dazu betrieben worden ist; für eine Übersicht siehe zum Beispiel Facca und Lanzi, Minining interesting knowledge from weblogs: a survey, aus dem Jahr 2004 (2005 veröffentlicht). Wurden früher vor allem Weblogs (nicht Web-Blogs!) verwendet, also vom Server geschriebene Logdateien, so haben wir heute durch Google Analytics & Co die Möglichkeit, viel “bessere” Daten verwenden zu können.
Aber was genau ist besser? Wir können in GA & Co besser Menschen von Bots unterscheiden (von denen es mehr gibt als man denkt), Wiederkehrer werden zuverlässiger erkannt, Geräte etc. Die Frage ist, ob man die zusätzlichen Daten unbedingt verwenden muss für grundlegende datengetriebene Personas. Denn Assoziationsregeln, über die ich schon mal in einem Beitrag über das Clustering mit Google Analytics und R geschrieben habe und die auch von Facca und Lanzi erwähnt werden, können bereits grundlegende Gruppen von Nutzer identifizieren (ich hatte in dem anderen Artikel bereits erwähnt, dass ich für einen der Schöpfer des Algos, Tomasz Imilinski, mal gearbeitet hatte, aber eine Anekdote mit ihm muss ich noch loswerden: In einem Meeting sagte er mal zu mir, dass man oft denke, etwas sei eine low hanging fruit, ein schneller Erfolg, aber, “Tom, often enough, the low hanging fruits are rotten”. Er hat damit so oft Recht behalten.). Die Gruppen identifizieren sich durch ein gemeinsames Verhalten, die Co-Occurence von Seitenaufrufen zum Beispiel. In R funktioniert das wunderbar mit dem Package arules und dem darin enthaltenen Algo apriori.
Wie bereits in dem früheren Artikel erwähnt: Eine Standard-Installation von Google Analytics ist nicht ausreichend (ist sie sowieso nie). Entweder hat man die 360-Variante oder “hackt” die kostenlose Version (“hacken” in Bezug auf “tüftlen”, nicht “kriminell sein”) und zieht sich die Daten via API. Bei Adobe Analytics können die Daten aus dem Data Warehouse gezogen werden oder auch über eine API. Einfach Google Analytics verwenden und daraus Personas ziehen ist also nicht möglich bei diesem Ansatz. Man muss außerdem nachdenken, welches Datum aus GA am besten verwendet wird neben der Client ID, um Transaktionen zu repräsentieren. Das kann von Website zu Website ganz unterschiedlich sein. Und wenn man ganz geschickt sein will, dann ist ein PageView allein vielleicht nicht Signal genug.
Hier geht es aber zunächst um die Visualisierung und welche Einschränkung der apriori-Ansatz hat für die automatisierte Generierung von datengetriebenen Personas. Für die Visualisierung arbeite ich mit dem Package arulesViz. Die daraus entstehenden Grafiken sind nicht ganz einfach zu interpretieren, wie ich an der HAW, aber auch mit Kollegen erlebt habe. Wir sehen hier unten die Visualisierung von Assoziationsregeln, die aus den Daten dieser Seite gewonnen werden, und zwar mit dem GA-Datum pagePathLevel1 (der bei mir leider gleichzeitig ein Artikel-Titel ist). Hier fällt bereits eines auf: Ich kann hier eigentlich nur zwei Gruppen identifizieren, und das ist ganz schön dürftig.
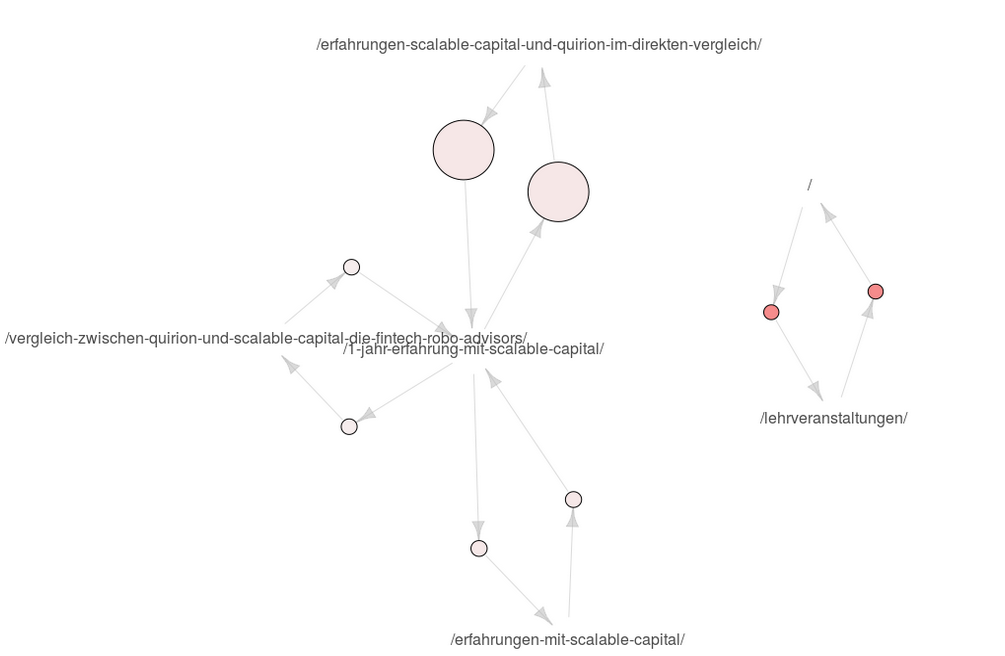
Was sehen wir hier genau? Wir sehen, dass Nutzer, die auf der Homepage sind, auch in den Bereich Lehrveranstaltungen gehen und umgekehrt. Der Lift ist hier hoch, der Support nicht so. Und dann sehen wir, dass sich Nutzer zwischen meinen vier Artikeln über Scalable Capital bewegen, mit ungefähr gleichem niedrigen Lift, aber unterschiedlich hohem Support. Lift ist der Faktor, um den die Co-Occurence von zwei Items höher ist als deren wahrscheinliches Auftreten, wenn sie unabhängig voneinander wären. Support ist die Häufigkeit. Der Support war beim Erstellen der Assoziationsregeln auf 0.01 definiert worden, die Konfidenz ebenso auf 0.01. Für Details siehe meinen ersten Artikel.
Warum aber sehe ich hier keine anderen Seiten? Mein Artikel über Google Trends ist ein sehr häufig gelesener Artikel, ebenso der über den Thermomix oder AirBnB. Es liegt also nicht daran, dass es nicht mehr Nutzergruppen gäbe. Der Nachteil dieses Ansatzes ist einfach, dass Nutzer mehr als eine Seite besucht haben müssen, damit überhaupt eine Regel hier entstehen kann. Und da einige Nutzer über eine Google-Suche kommen und anscheinend kein Interesse an einem zweiten Artikel haben, weil ihr Informationsbedürfnis vielleicht schon befriedigt ist oder weil ich diese nicht gut genug anpreise, sind hier in diesen Regeln anscheinend nur Studierende sowie Scalable Capital-Interessierte zu identifizieren.
Bisher habe ich drei Lösungswege für dieses Dilemma identifiziert, und alle erfordern Mehrarbeit:
Am schönsten ist der erste Ansatz, meiner Meinung nach, aber dieser erfordert Zeit und Gehirn. Und dass etwas herauskommt ist nicht gesagt. Der letzte Ansatz ist unschön, da wir hier halt mit Fällen zu tun haben, die seltener vorkommen und daher nicht unbedingt belastbar. Bei einem Support von 0.005 sieht die Visualisierung zwar anders aus:

Aber wieder habe ich das Problem, dass die Einzelseiten nicht auftauchen. Es ist also anscheinend extrem selten, dass sich jemand von dem Google Trends-Artikel zu einem anderen Artikel hinbewegt, so dass das Herabsenken des Support-Werts nix gebracht hat. Aus der Erfahrung kann ich sagen, dass dieses Problem mehr oder weniger stark auftaucht auf den meisten Seiten, die ich ansonsten sehe, aber es taucht immer irgendwie auf. Das Dumme ist, wenn man schon gute Personas ablesen kann, dann ist man eher geneigt, sich den Rest nicht mehr anzusehen, auch wenn der vom Umfang her sehr groß sein könnte.
Wir sehen in der Grafik außerdem ein weiteres Problem, denn die Nutzer im rechten Strang müssen von Pfeil zu Pfeil nicht dieselben sein. Anders ausgedrückt: Es ist nicht gesagt, dass sich Besucher, die Fotografie-Seiten und Lehrveranstaltungen ansehen, auch die Veröffentlichungen ansehen, auch wenn das in der Visualisierung so aussieht. Wenn A und B sowie B und C, dann gilt hier nicht A und C! Um dies zu lösen, müssten die Assoziationsregeln in der Visualisierung noch eine ausschließende Kennzeichnung haben. Die existiert nicht und wäre eine Aufgabe für die Zukunft.
Der Weg über Assoziationsregeln ist spannend für die Erstellung Daten-getriebener Personas mit Google Analytics oder anderen Webanalyse-Tools. Er wird momentan in der Regel aber nicht ausreichend sein, da a) das Problem von Eine-Seite-Besuchern hier nicht gelöst wird, b) die Regeln nicht ausreichend über unterschiedliche Gruppen informieren, die nur Überschneidungen haben und c) er eh nur über diejenigen Gruppen etwas aussagen kann, die bereits auf der Seite sind. An a) und b) arbeite ich momentan nebenbei, über Gedanken von außen freue ich mich dabei immer
Google Optimize ist eines meiner Lieblings-Tools, denn es ermöglicht jedem schnell a/b-Tests zu bauen; in meinen Kursen staunen die Teilnehmer häufig, wie schnell so ein Test online sein kann. Natürlich ist die Vorarbeit, das saubere Erstellen einer Hypothese, nicht so schnell getan, aber es macht auch keinen Spaß, monatelang auf die Live-Schaltung eines Tests zu warten. Über die Vorzüge von Google Optimize will ich auch gar nicht weiter eingehen, sondern stattdessen auf drei Feinheiten hinweisen, die nicht so offensichtlich sind.
Die Google Analytics API erlaubt auch den Zugriff auf Google Optimize-Daten, die in Analytics reinlaufen, was ermöglicht, dass die Analytics-Rohdaten zu einem Google Optimize-Test analysiert werden können. Das ist vor allem dann interessant, wenn etwas nicht als KPI in Optimize verwendet werden kann, man in Google Optimize vergessen hat, einen KPI einzustellen oder Nebeneffekte analysiert werden sollen. Einiges davon geht auch hinterher mit Segmenten, aber hey, hier geht es ums Hacken (im Sinne von Tüftler, nicht Krimineller), da macht man auch Dinge, weil man sie machen kann, nicht weil sie immer notwendig sind

Die beiden wichtigen Optimize-Dimensionen heißen ga:experimentId und ga:experimentVariant, mittlerweile existiert auch eine Kombination, die ga:experimentCombination heißt. Wobei, wenn man nur einen Test fährt, dann reicht es auch, nur die Dimension ga:experimentVariant abzufragen. 0 ist die Originalvariante (Kontrollgruppe), danach wird pro Variante hochgezählt. Hat man mehrere Tests am laufen, so einfach in der Google Optimize-Oberfläche die ID nachschauen; sie findet sich in der rechten Spalte unter Google Analytics. Sie ist meistens sehr kryptisch, wie man auf dem Bild sehen kann.

In meinem Beispiel habe ich zwei Experimente am Laufen, so dass ich mir die Kombination ausgeben lasse neben drei Custom Dimensions (Client ID, Hit Type und UNIX Timestamp) sowie Seitentitel (die Client ID hab ich auf dem Bild etwas abgeschnitten, da es ja nur ein pseudonymisiertes Datum ist). Wir sehen auf dem zweiten Bild die beiden Experimente und die jeweiligen Varianten in einem Feld. In dem Test, der mit c-M startet, hatte ein Kursteilnehmer die Hypothese aufgestellt, dass die Besucher meiner Seite mehr Seiten ansähen und mehr Zeit verbrächten, wenn das Suchfenster weiter oben wäre. Ich habe nicht daran geglaubt, aber Glauben ist nicht Wissen, also haben wir den Test gefahren mit dem KPI Session Duration. Vergessen hatte ich hier, die Anzahl der Suchen als zweiten KPI einzustellen. Nun gut, dass ich die Rohdaten habe, auch wenn ich dafür natürlich auch ein Segment bauen könnte.
Wie wir in dem Screenshot auch sehen können, sind die Nutzer gleichzeitig in zwei Tests, da der andere Test keinen Einfluss auf den ersten Test haben sollte. Nun gab es während der Test-Laufzeit von 4 Wochen auf meiner Seite nur 3 Nutzer, die nach etwas gesucht haben, einer der Nutzer hat eine Query mehrmals gesucht, ein Nutzer hat zwei verschiedene Terme gesucht. Bei einer so geringen Fallzahl brauchen wir erst gar nicht über Signifikanz nachdenken. Zwischenzeitlich sah es mal so aus, als würde tatsächlich die Suchfenster oben-Variante gewinnen, aber dazu im letzten Abschnitt mehr. Die Frage ist nun, warum überhaupt die Variante besser sein kann, wenn doch kaum gesucht wurde? Oder hat allein die Präsenz der Suchbox zu einer längeren Session Duration geführt? Sehr unwahrscheinlich!

Das sollten wir uns einmal genauer anschauen…
Zu beachten ist in den Rohdaten, dass es nun für jeden Hit eines Nutzers zwei Einträge gibt, einen pro Test. Außerdem wird nicht jeder Nutzer in einem Test sein, auch wenn 100% des Traffics getargeted sind, was man aber auch schon in Google Analytics sehen kann. Ebenso können wir überprüfen, ob durch die zufällige Auswahl von Test- und Kontrolgruppenteilnehmern eine einigermaßen gleichmäßige Aufteilung der Nutzer erfolgt ist (z.B. Mobile versus Desktop etc). Auch das ist natürlich mit dem Interface möglich.
Das erste, was auffällt, wenn ich die Daten aus der API ziehe, ist, dass die Werte nicht mit denen aus der GUI übereinstimmen. Das ist zunächst einmal ziemlich beunruhigend. Schaue ich mir nur Users und Sessions an, so stimmen die Werte genau überein. Nehme ich die Dimension experimentCombination hinzu, so passen die Zahlen nicht mehr, und es liegt nicht an den Unterschieden zwischen API v3 und v4. Es ist nicht ungewöhnlich, dass die Daten nicht zusammen passen, meistens geschieht das durch Sampling, aber das kann hier nicht der Fall sein. Interessanterweise stimmen auch die Zahlen innerhalb der GUI nicht überein, wenn ich mir die Daten unter Experiments ansehe und sie mit dem Dashboard zur Zielgruppe vergleiche. Die Zahlen aus der API stimmen aber mit den Daten aus dem Experiments-Bericht überein. Vorsicht also wer Segmente bildet!
Ziehe ich die Daten inklusive meiner ClientID-Dimension, so habe ich etwas weniger Users, was sich dadurch erklärt, dass nicht jeder User eine solche ID in die Custom Dimension reinschreibt, d.h. er hat diese Client ID wahrscheinlich (oder sicherlich, denn sonst könnte GA ihn nicht als einzelnen Nutzer identifizieren), aber ich schaffe es irgendwie nicht die ID in die Dimension zu schreiben, so dass dort zB “False” steht.
Nun schauen wir uns einmal ein paar Daten an. Mich interessiert zum Beispiel, ob Optimize es schafft, die gleiche Verteilung über Devices hinzubekommen wie ich sie auf der Seite habe:

Der Großteil meines Traffics findet noch auf dem Desktop statt. Wie sieht es in Optimize aus?

Die Verteilung ist definitiv eine andere. Das ist auch wenig verwundertlich, denn auf AMP-Seiten sollte kein Optimize-Experiment ausgespielt werden; es ist also eher verwunderlich, warum hier überhaupt noch Experimente auf Mobilgeräten stattgefunden haben. Und diese Fälle haben andere Werte in Bezug auf den Ziel-KPI, wie man auch in Analytics sehen kann:

Wir können also nicht von den Testergebnissen auf die ganze Seite schließen, wir wissen aber auch nicht, wie groß der Effekt der unerwarteten Mobile-User auf das Testergebnis ist. Hierzu müssten wir also den Gewinner neu ermitteln. Doch wie wird der Gewinner überhaupt ermittelt? Wir könnten zum Beispiel einen Chi-Square-Test verwenden mit der Beobachtung der durchschnittlichen SessionDuration:
chisq.test(x) Pearson’s Chi-squared test with Yates‘ continuity correction data: x X-squared = 1.5037, df = 1, p-value = 0.2201`
In diesem Fall ist p über 0.05, zu p im nächsten Abschnitt mehr. Sollte der Chi-Square-Test überhaupt der richtige Test sein, so ergäbe er, dass der Unterschied nicht statistisch signifikant ist. Allerdings ist das nicht der Test, den Google Optimize verwendet.
Was passiert da eigentlich genau unter der Motorhaube? Schauen wir uns an, wie Google Optimize berechnet, ob eine Variante gewonnen hat oder nicht. Im Gegensatz zu Adobe Test & Target zum Beispiel oder den meisten Signifikanzrechnern wie dem von Konversionskraft (wobei Konversionskraft nicht mal sagt, was für einen Test sie nutzen), basiert Google Optimize nicht auf einem t-Test, Mann-Whitney-U- oder Chi Square-Test, sondern auf einem Bayes-Inferenz-Verfahren. Was bedeutet das?
Hier treffen zwei unterschiedliche Vorstellungen aufeinander, die der sogenannten Frequentists (NHST steht für Null Hypothesis Significance Testing) und die der Bayesschen Inferenz-Anhänger. Diese wurden und werden zum Teil immer noch in der Statistik intensiv diskutiert, und ich bin nicht der Richtige, um hier ein Urteil zu fällen. Aber ich versuche, diese beiden Ansätze für Nicht-Statistiker zu beleuchten.
In den meisten A/B-Test-Tools werden Hypothesen-Tests durchgeführt. Man hat zwei Gruppen von ungefähr gleicher Größe, die eine Gruppe wird einem “Treatment” ausgesetzt, und dann wird beobachtet, ob sich der definierte KPI in der Testgruppe “signifikant” ändert. Für Signifikanz wird meistens auf den p-Wert geschaut; sofern dieser unter 0,05 liegt oder wie auch immer das Signifikanz-Niveau definiert wurde, wird die Null-Hypothese abgelehnt. Zwar sieht man auf den Tool-Oberflächen nichts von Null-Hypothesen etc, wahrscheinlich um die Nutzer nicht zu verwirren, aber das Denkkonstrukt dahinter geht davon aus. Wird zum Beispiel getestet, ob ein roter Button häufiger angeklickt wird als ein blauer, so würde die Null-Hypothese lauten, dass beide gleich häufig angeklickt werden. Der Hintergrund davon ist, dass sich eine Hypothese nicht immer belegen lässt. Wenn aber das Gegenteil der Hypothese eher unwahrscheinlich ist, so kann angenommen werden, dass eine Hypothese eher wahrscheinlich ist. Von nichts anderem handelt der p-Wert.
Nun ist der p-Wert keine einfache Geschichte, nicht einmal Wissenschaftler schaffen es, den p-Wert so zu erklären, dass es verständlich ist, und es wird diskutiert, ob er überhaupt sinnvoll ist. Der p-Wert sagt nichts darüber aus, wie “wahr” ein Testergebnis ist. Er sagt lediglich etwas darüber aus, wie wahrscheinlich es ist, dass dieses Ergebnis auftritt, wenn die Null-Hypothese wahr ist. Bei einem p-Wert von 0,03 bedeutet das also, dass die Wahrscheinlichkeit, dass ein Ergebnis auftritt bei einer wahren Null-Hypothese, bei 3% liegt. Das bedeutet umgekehrt nicht, wie “wahr” die Alternative Hypothese ist. Der umgekehrte p-Wert (97%) bedeutet also nicht eine Wahrscheinlichkeit, dass eine Variante eine andere Variante schlägt.
Ein häufiges Problem mit a/b-Tests ist zudem, dass die Sample-Größe nicht vorher definiert wird. Der p-Wert kann sich über die Laufzeit eines Experiments ändern, und so können statistisch signifikante Ergebnisse nach ein paar Tagen schon nicht mehr signifikant sein, da sich die Anzahl der Fälle geändert hat. Außerdem interessiert nicht nur die Signifikanz, sondern auch die Stärke/Trennschärfe/Power eines Tests, die nur in den wenigsten Test-Tools angezeigt wird.
Das sind aber vor allem Probleme der Tools, nicht des Frequentists-Ansatzes, der von den meisten Tools genutzt wird. Das “Problem” des Frequentists-Ansatzes ist, dass sich ein Modell nicht ändert, wenn neue Daten hereinkommen. So kann bei wiederkehrenden Besuchern eine Änderung auf der Seite irgendwann gelernt werden, so dass ein anfänglicher a/b-Test zwar große Wirkung prophezeit, die tatsächliche Wirkung aber viel geringer ist, weil im Frequentists-Ansatz einfach nur die Gesamtzahl von Conversions gezählt wird, nicht die Entwicklung. In der Bayesschen Inferenz werden neu hereinkommende Daten aber berücksichtigt, um das Modell zu verfeinern; geringer werdende Conversion-Raten würden das Modell beeinflussen. Daten, die sozusagen “vorher” vorhanden sind und die Annahmen über den Einfluss in einem Experiment beeinflussen, werden Anfangswahrscheinlichkeit oder “Priors” genannt (ich schreibe Priors, weils schneller geht). Das Beispiel in der Google-Hilfe (das auch anderswo gerne bemüht wird), ist, dass, wenn man sein Handy im Haus verlegt, nach der Bayesschen Inferenz das Wissen, dass man sein Handy gerne mal im Schlafzimmer vergisst, verwenden und auch einem Klingeln “hinterherlaufen” darf. Bei den Frequentists darf man das nicht.
Und hier genau tut sich das Problem auf: Woher wissen wir, dass die “Priors” relevant sind für unsere aktuelle Fragestellung? Oder, wie es im Optimizely-Blog gesagt wird:
The prior information you have today may not be equally applicable in the future.
Die spannende Frage ist nun, wie Google in Optimize auf die Priors kommt? Dazu wird folgende Aussage gemacht:
Despite the nomenclature, however, priors don’t necessarily come from previous data; they’re simply used as logical inputs into our modeling.
Many of the priors we use are uninformative – in other words, they don’t affect the results much. We use uninformative priors for conversion rates, for example, because we don’t assume that we know how a new variant is going to perform before we’ve seen any data for it.
An diesen beiden Blogauszügen wird schon deutlich, wie unterschiedlich das Verständnis von der Nützlichkeit der Bayesschen Inferenz ist Gleichzeitig ist offensichtlich, dass uns wie in jedem anderen Tool auch Transparenz darüber fehlt, wie genau die Berechnungen zustande gekommen sind. Ein weiterer Grund, dass man, wenn man auf Nummer sicher gehen will, die Rohdaten benötigt, um eigene Tests durchzuführen.
Der Bayes-Ansatz erfordert mehr Rechenzeit, was wahrscheinlich der Grund dafür ist, dass die meisten Tools nicht diesen Ansatz nutzen. Es existiert auch Kritik an der Bayes-Inferenz. Das Hauptproblem aber ist, dass die meisten Nutzer viel zu wenig wissen von dem, was genau die a/b-Test-Tools tun und wie belastbar die Ergebnisse sind.
Nun stellt sich die Frage, warum überhaupt ein Unterschied sichtbar war bei der Session Duration, wenn doch kaum jemand gesucht hat. Hier kann ein A/A-Test helfen. A/A-Test? Richtig gelesen. Auch sowas gibt es. Und ein solcher Test hilft dabei, die Varianz der eigenen Seite zu identifizieren. So hatte ich einen wunderbaren Test, bei dem ich die AdSense-Klickrate nach einer Design-Änderung getestet hatte. Die Änderung war sehr erfolgreich. Um ganz sicher zu gehen habe ich noch mal getestet; dieses Mal hatte die Änderung schlechtere Werte. Nun kann es natürlich sein, dass einfach schlechtere Ads geschaltet wurden und sich deswegen die Klickrate verschlechtert hatte. Es könnte aber auch einfach sein, dass die Seite selber eine Varianz hat. Und diese kann man herausfinden, indem man einen A/A-Test fährt (oder die vergangenen Rohdaten für einen solchen Test nutzt). Bei so einem Test wird in der Test-Variante einfach nichts geändert und dann geschaut, ob sich einer der Haupt-KPIs ändert oder nicht. Rein theoretisch sollte sich nichts ändern. Aber wenn doch? Dann habe wir eine Varianz identifiziert, die in der Seite und dem Traffic selbst liegt. Und die wir in zukünftigen Tests berücksichtigen sollten.
Vorab: Ich bin kein komplett ausgebildeter Statistiker oder Marktforscher. Zwar beschäftige ich mich leidenschaftlich mit Zahlen und versinke auch in meiner Freizeit in Statistikbüchern, aber je mehr man weiß, desto mehr weiß man, was man nicht weiß. Die Weisheit habe ich nicht mit Löffeln gefressen, und ich bin immer dankbar, wenn Schlauere Feedback geben. Ich glaube aber, dass jeder einigermaßen klar denkende Mensch ohne Statistik-Grundkurs verstehen kann, wann Daten nicht sinnvoll erhoben wurden oder falsche Ableitungen erstellt werden.

Auf diese These bin ich durch die Postings von Andre Alpar und Karl Kratz aufmerksam geworden. Sie stammt von Best4Planning, hier die ganze Studie “Qualität ist wichtiger als Likes”. Anders als die sehr geschätzen Kollegen Andre und Karl halte ich best4planning nicht für eine Satireseite, die b4p-Ableitung aus den Daten aber für zumindest mutig. Wenn man jetzt mal von den Haarwuchsmitteln in den Kleinanzeigen einer Zeitung absieht, die typische “10 Kilo in 2 Tagen abnehmen” oder “Millionäre wollen nicht, dass sie dieses Video sehen”-Reklame auf Facebook & Co spricht nicht für Social. Zumindest subjektiv würde ich die These also bestätigen. Die Eintrittshürde für Werbung im Netz ist wunderbar niedrig, in Print kostet sie nun mal vorab viel Geld. Ob die Automotive-Werbung für sauberen Diesel in Print heute noch als glaubwürdig wahrgenommen wird lassen wir mal dahingestellt, aber jeder Idiot kann in Online-Medien für wenig Geld ein Produkt anbieten. Von daher würde ich die Daten aus b4p, dass Werbung in Print glaubwürdiger ist, nicht anfechten.
Anders sieht es mit der Interpretation aus. Ist glaubwürdig gleichzusetzen mit kaufanregender? Ich halte das zunächst für eine Misinterpretation der Daten. Doch das Problem liegt meiner Meinung nach an der Grafik, denn als Quelle wird das Glaubwürdigkeits-Merkmal genannt: Es gibt auch das Merkmal “kaufanregend”:

So ergibt das also Sinn. Ich weiß zwar nicht, wie sie jetzt auf 28,1% gekommen sind, da ich unter Print sowohl Tageszeitungen als auch Magazine etc verstehe, aber vielleicht haben sie einfach (34+22)/2 gerechnet und sind somit auf die Zahl gekommen (intern werden sie wohl Nachkommastellen haben). Wie auch immer, die Erklärung in der Grafik ist unglücklich. Denn so denkt man (also ich zumindest), dass aus vertrauenswürdig das Merkmal kaufanregend abgeleitet wird.
Gehen wir mal einen Schritt weiter. Die Daten sind über alle Altersstufen verteilt, wie sieht es aus, wenn wir mal nach Altersklassen teilen?

Wow. Der demographische Faktor hat anscheinend gut zugeschlagen. Wenn ich jetzt nicht alles falsch gemacht habe, dann stimmt die Aussage, dass Ältere Werbung in Print vertrauenswürdiger und kaufanregender finden, Jüngere eher in Social Media. Wie bei Karl auf FB bereits kommentiert sind 65% der Befragten mindestens 40 Jahre alt, 49% mindestens 50, da unter 14 nicht befragt wird. Wir haben also einen Überhang der Älteren, die auch eher Print nutzen. Nun sind die unter 14-Jährigen natürlich nicht so stark in Social vertreten und auch nicht in Print, aber die Altersentwicklung in DE tut ihr Übriges dazu, dass die Zahl so stimmen mag. Das wird uns Hardcore-Onlinern nicht gefallen, lieber Andre, lieber Karl, aber außerhalb unserer Bubble sind tatsächlich Menschen, die keine telepathische Verbindung ins Netz haben.
Wenn man noch mal genauer hinschaut: 28.1% der Befragten finden laut Grafik Werbung in Print glaubwürdig. 28.1%. Das ist weniger als ein Drittel. Letztendlich könnte man auch sagen, Joa, Werbung bei Print ist für die Mehrheit der Befragten nicht glaubwürdig, aber bei Social noch viel weniger!
Fazit: Zahlen ok, Interpretation schwierig, wenn man es nicht differenziert sieht. Die Aufregung um die Aussage ist zu verstehen, denn sie stimmt zwar, aber ein Durchschnitt über die Gesamtpopulation ist immer noch ein Durchschnitt, und der ist in der Regel suboptimal, da er nichts über die Verteilung sagt.
Nun kann man mit b4p auch viel Mist machen. Vor allem dann, wenn man nicht versteht, wie die Daten gesammelt werden. Aber das haben wir auch bei Google Trends. Oder bei Similar Web. A fool with a tool is a fool. Punkt. Natürlich können wir es uns einfach machen und sagen, dass sowieso jede Marktforschung gelogen ist, aber das wäre nicht fair, denn es gibt genug Marktforscher, die sich verdammt viel Mühe geben.
Wie aber entstehen die Daten von b4p? Tatsächlich wurden für diese Studie 30.121 Menschen befragt, das sind sehr viel mehr Menschen als die in der Einschaltquote Beteiligten, zu denen ich auch mal gehört hatte, und es ist eine gute Basis. Hierzu gab es zwei Befragungswellen, alles hier nachzulesen. Ich sehe keinen Grund, das anzuzweifeln, nur weil Verlage die Auftraggeber sind. Denn man kann in den Daten auch so rumwühlen, dass manches nicht so wirklich schick aussieht für Print.
Die technische Messung fand mit 10.231 Teilnehmern im GfK Crossmedia Link Panel statt, denen auch eine anscheinend etwas gekürzte Form des Fragebogens zugeschickt wurde. Dann wurden diese Daten aus dem Panel und den Interviews sozusagen “übereinander” gelegt. Das ist ein übliches Verfahren. Daraus ergeben sich aber auch Konsequenzen. Beispiel: Ich baue mir eine Zielgruppe in b4p aus Menschen über 50, die selbständig sind in einem Baubetrieb usw. Aus n=30.121 wird dann ganz schnell n=12, die befragt wurden. Das ist schon schwierig, aber nun gut. Wenn ich mir dann aber die Mediennutzung ansehe, dann kann es sein, dass diese ja aus dem Drittel der Befragten des GfK-Panels stammt, also müsste ich korrekterweise 12:3 rechnen und wäre bei 4. Schwierig. Leider sagt die b4p-Seite nichts über solche Fälle, gibt keinerlei Hilfestellungen. Aber ich würde meine Werbe-Millionen nicht auf Basis solcher Daten investieren, wenn n so klein ist. Bedeutet das, dass b4p unseriös ist? Nein. Das Problem sitzt vor dem Bildschirm, denn die kleine Zahl links oben, die für die Fallzahl steht, ist nun mal sehr klein und wird deswegen auch gerne mal übersehen. Was wäre auch die Alternative? Gar nichts?
Wo ich tatsächlich Bauchweh habe, das sind die Fragen, zumindest die, die veröffentlicht sind, und da habe ich nur eine gefunden: “Denken Sie nun einmal an die Tage von Montag bis Samstag. An wie vielen von diesen 6 Werktagen sehen Sie im Allgemeinen morgens zwischen 6:00 Uhr und 9:00 Uhr Sendungen im Fernsehen? Denken Sie bitte auch daran, dass der Samstag oft anders abläuft als die anderen Werktage”. Aufgrund der sozialen Erwünschtheit: Wer mit ausreichend Gehirnzellen gibt denn freiwillig zu, dass er sich morgens schon mit Frühstücksfernsehen zuballert? Ich hoffe aber, dass solche Fragen durch weitere Kontrollfragen abgesichert sind.
Fazit: b4p ist für viele Anliegen eine gute Anlaufstelle. Wichtig ist, die Daten mit anderen Datenquellen und dem gesunden Menschenverstand abzusichern.
Gibt es Alternativen zu b4p? Wenige. Manche schwören auf Statista, aber bei der unreflektierten Nutzung von Befragungen stirbt ebenso ein Statistik-Einhorn wie bei b4p (das ist der Grund, warum Ihr keine Einhörner mehr seht). Statista ist natürlich eine extrem coole Seite mit tollen Daten, aber auch hier lohnt sich ein Blick in die Details, von wem die Studie eigentlich stammt. Zum Beispiel diese Studie vom Februar 2018, die uns sagt, dass 14% der mindestens 60-Jährigen auf Pinterest sind. Auch 14% der 50-59-Jährigen. n bei beiden Gruppen um die 600. Wow. Klingt super für Pinterest. Dummerweise muss man für Statista zahlen, wenn man die Quelle haben will, aber das hat netterweise jemand für mich getan. Die ganze Studie stammt vom Faktenkontor. Erhebung durch Toluna. Toluna? Was ist das? Eine Webseite, auf der man etwas dafür bekommt, wenn man an Umfragen teilnimmt. Hm. Wir haben also nicht zufällig aus den mindestens 60-Jährigen Menschen ausgewählt, die wir befragen, sondern einfach nur die genommen, die eh schon online sind und dann auch noch dieses Portal kennen usw. Dumm nur, dass nur 55% der über 65-Jährigen überhaupt im Internet sind laut destatis. Wir haben also eine eh schon online-affine Gruppe befragt, deren Wahrscheinlichkeit bei Pinterest zu sein dementsprechend höher ist. Ich wäre zumindest sehr vorsichtig, bei Rentnern als Zielgruppe nun Pinterest zu empfehlen und diese Zahl von 14% irgendwo zu verwenden.
Fazit: Schau Dir genau an, wie die Daten erhoben wurden.
Das Problem sind nicht die Daten, solange man versteht, woher sie kommen und wie sie erhoben wurden. Aber das will man gar nicht genau wissen manchmal, weil man eine Meinung hat und sich diese dadurch belegt, dass man nur die Daten auswählt, die die eigene Meinung bestätigen (und da bin ich nicht von ausgenommen). Man nennt das den Bestätigungsfehler. Darüber habe ich auch an anderer Stelle schon mal geschrieben. Oder man hat nicht die Zeit, Daten zu überprüfen. Oder manchmal auch nicht den Willen. Man sieht nur eine Zahl, hat eine eigene Meinung und schießt dann los. Ich wünsche mir manchmal mehr Differenzierung. So mal ganz nebenbei. Aber einfache Antworten sind immer besser zu kommunizieren.
Übrigens, ein schönes Buch, das ich gerade lese: Thomas Bausch – Stichprobenverfahren in der Marktforschung. Gibts gebraucht für weniger als 5€ bei Amazon.
Wer hier öfter mitliest, der weiß, dass Sistrix eines meiner absoluten Lieblings-Tools ist (ich verlinke mal ganz dreist als bestes SEO Tool), allein schon wegen der schlanken API, dem absolut liebenswürdigen Johannes mit seinen wirklich schlauen Blog-Posts sowie der Unaufgeregtheit, mit der die Toolbox immer wieder überzeugt. Natürlich sind auch alle anderen Tools klasse, aber Sistrix ist sowas wie meine erste große Tool-Liebe, die man nicht aus seinem SEO-Gedächtnis verbannen kann oder will. Und auch wenn die folgenden Daten eventuell am Lack kratzen könnten, eine richtige Delle haben sie in meiner Sistrix-Präferenz nicht verursacht.
Aber genug der Lobhudelei. Worum gehts? Wie schon in dem Post über keywordtools.io oder den am Rande erwähnten Ungenauigkeiten in den Google AdWords Keyword Planner-Daten beschrieben, ist es eine Herausforderung, verlässliche Daten über das Suchvolumen von Keywords zu bekommen. Und wer immer noch glaubt, dass Google Trends absolute Zahlen liefert, nun ja… Sistrix bietet hierfür einen Traffic-Index von 0-100, der auf Basis von verschiedenen Datenquellen berechnet wird, womit eine höhere Genauigkeit entstehen soll. Doch wie genau sind die Zahlen hier? Nebenbei will ich außerdem zeigen, warum Boxplot ein wunderbarer Weg sind, Daten zu visualisieren.
Als Datenbasis dienen hier 4.491 Suchanfragen aus einem Sample, wo ich sowohl die Sistrix- als auch die Google AdWords Keyword Planner-Daten habe. Es ist übrigens nicht das erste Sample, was ich gezogen habe, und die Daten sehen überall ungefähr gleich aus. Es liegt also nicht an meinem Sample. Schauen wir uns also zunächst einmal die reinen Daten an:

Wie wir sehen, könnte man eine Kurve in diesen Plot hineinzeichnen, die Relation scheint schon mal nicht linear zu sein. Aber vielleicht haben wir es hier nur wegen des Ausreißers ein verzerrtes Bild? Schauen wir uns den Plot ohne den Riesen-Ausreißer an:

Vielleicht haben wir hier immer noch zu viele Ausreißer, wir nehmen mal nur die unter einem Suchvolumen von 100.000 pro Monat:

Tatsächlich sehen wir hier eine Tendenz, dass es rechts weiter nach oben geht, zwar keine deutliche Linie (ich habe auf eine Regressionsanalyse verzichtet), aber wir sehen auch, dass wir bei einem Traffic-Wert von 5 Werte haben, die über die Indexwerte von 10,15,20,25 und 30 hinausgehen, sogar bei 50. Schauen wir uns das arithmetische Mittel der Suchvolumina an (mit Ausreißern), so sehen wir wieder die Kurve:

Der Median ignoriert die Ausreißer innerhalb der kleineren Werte:

Sehen wir uns die Daten also im Median an, so sehen wir zumindest bei den höheren Werten eine korrekte Tendenz mit Ausnahme des Wertes bei dem Sistrix-Traffic-Wert von 65 oder 70. Allerdings ist die Streuung um diese Werte sehr unterschiedlich, wenn man die Standardabweichungen für jeden Sistrix-Traffic-Wert plottet:

In der Streuung sehen wir kein Muster. Es ist nicht so, dass die Streuung mit einem höheren Index-Wert zunimmt (was zu erwarten wäre), tatsächlich ist sie bei dem Index-Wert von 5 schon höher als bei 10 etc. Die höchste Streuung sehen wir bei dem Wert von 60.
Weil Boxplots einfach eine wunderbare Angelegenheit sind, schieße ich den auch noch hinterher:

Hier sind die Daten einmal umgedreht (weil sie mit den Sistrix-Daten auf der X-Achse nicht wirklich gut erkennbar waren). Die Box zeigt jeweils an, wo 50% der Daten liegen, also bei einem Suchvolumen von 390 zum Beispiel liegen 50% der Daten zwischen dem Sistrix-Wert von 5 und 25 zu liegen, der Median wird durch den Strich in der Box gekennzeichnet und liegt bei 15. Die Größen der Boxen nehmen am Anfang zu, danach sind sie wieder unterschiedlich groß, was auf eine geringere Streuung hinweist. Bei manchen Datenpunkten sehen wir kleine Kreise, die R als Ausreißer berechnet hat. Wir sehen also gerade bei den geringen Suchvolumina Ausreißer. Fast alles, was wir oben geplottet hatten, kriegen wir hier in einem Plot visualisiert. Boxplots sind einfach wunderbar.
Bedeutet das nun, dass die Traffic-Daten in Sistrix unbrauchbar sind? Nein, das bedeutet es nicht. Denn wie in der Einleitung beschrieben sind auch die Keyword Planner-Daten nicht immer korrekt. Nichts Genaues weiß man also nicht. Wer die Keyword Planner-Daten als Nonplus-Ultra sieht, der wird sich mit den Sistrix-Daten nicht zufrieden geben können. Hilfreich wäre, wenn es mehr Transparenz gäbe, wo die Daten genau herkommen. Offensichtlich wären angebundene GSC-Daten sehr hilfreich, da sie echte Impressions zeigen. Meine Handlungsempfehlung ist, sich mehrere Datenquellen anzusehen und die Overlaps sowie die Abweichungen getrennt anzusehen. Das ist unbefriedigend, da es kein Automatismus ist. Aber “a fool with a tool is still a fool”.
Kommentare (seit Februar 2020 ist die Kommentarfunktion von meinem Blog entfernt):
Hanns says
Tom Alby says
martin says
Ich verstehe tatsächlich auch nicht, wie das technisch funktionieren soll. Wie soll Sistrix an die Suchanfragen kommen, die pro Keyword über Google laufen? Ist ja nicht so, als würde Google Sistrix bei jedem Request kurz informieren.
Das einzige was ich mir vorstellen kann ist, dass sie sich die Daten für jedes Keyword aus dem AdsPlanner ziehen. Aber … das als „eigenes Suchvolumen“ darzustellen, ohne Hinweis woher die Daten kommen, fände ich schon grob fahrlässig.
Woher könnten sie noch Daten bekommen?
Tom says
die Antwort ist halt nicht 1 oder 0, das kommt auch in dem Artikel heraus. Du kannst Dich auch nicht auf die AdPlanner-Daten verlassen. Sistrix bekommt auch noch Daten von Kunden, die die Search Console-Daten dort verknüpft haben, da Du ja die Impressions Deiner Seite für ein Keyword sehen kannst. Aber all das natürlich nicht für jedes Keyword. Und daher kommen Ungenauigkeiten zustande.
BG
Tom
Der letzte Teil dieser Serie über Suchmaschinenoptimierung/SEO und Data Science auf Basis meines Vortrags bei der SEO Campixx. Die Daten und den Code habe ich via Knit in ein HTML-Dokument überführt, das mein Notebook inklusive Daten nachvollziehbar macht. In dem Notebook sind auch ein paar mehr Untersuchungen drin, allerdings habe ich alles auf Englisch dokumentiert, da dies nicht nur für Deutsche interessant ist. Wer also alle Ergebnisse in einem Dokument lesen möchte (ohne die TF/IDF, WDF/IDF oder Stemming-Beispiele), schaut sich bitte das Data Science & SEO Notebook an. Speed und andere Faktoren sind in den vorherigen Teilen zu lesen.

Zunächst einmal ein Nachtrag: Uns fehlte ja das Alter für einige Domains, und diese Daten habe ich nun aus einer anderen Quelle bekommen. In unserem Sample waren die meisten Domains ja älter, und meine Sorge war, dass die fehlenden Domains eventuell sehr viel jünger waren und daher das Durchschnittsalter fälschlicherweise nach unten gezogen würde. Fast 20% der Domains fehlten.
Tatsächlich ist es so, dass die fehlenden Domains jünger sind. Lag der Median bei unserem löchrigen Datensatz bei 2001, liegt er bei den fehlenden Domains bei 2011. Führt man die Daten zusammen, liegt er aber dennoch wieder bei 2001, nur der Mean hat sich von 2002 auf 2003 geändert. Somit war die Anzahl der fehlenden Daten nicht so hoch, dass diese gegenläufige Tendenz einen großen Einfluss gehabt hätte. Natürlich könnte man nun entgegenhalten, dass diese andere Quelle einfach ganz andere Zahlen hat, aber bei einer Stichprobe der Domains, für die bereits ein Alter vorhanden war, konnte das nicht verifiziert werden. Und schaut man sich nun den Plot für die Beziehung zwischen Position auf der Suchergebnisseite und Alter einer Domain an, so haben wir also auch nichts Neues herausgefunden:

Boxplots sind eine wunderbare Angelegenheit, denn sie zeigen auf einen Blick unglaublich viel über die Daten. Die Box zeigt an, wo sich 50% der Daten befinden, der dicke Strich in der Mitte den Median, und die Breite der Box die Wurzel aus der Sample-Menge. Selbst nach mehreren Bier ist hier kein Muster zu erkennen, außer dass die Boxen alle ungefähr auf der gleichen Höhe sind. Google hatte ja bereits gesagt, dass das Alter einer Domain keine Rolle spielt.
Ein weiterer Mythos, und an diesem ist toll, dass wir ihn relativ einfach aufklären können, denn die Daten können wir uns selber crawlen. Übrigens eignet sich R nicht soooo super zum Crawlen; zwar gibt es das Paket rvest, aber wenn man wirklich nur den Content haben will, dann kommt nix an Pythons Beautiful Soup dran. Netterweise kann man in den RStudio-Notebooks auch Python ausführen Als Text wird hier also nur der tatsächliche Text genommen, nicht der Quellcode. Navigationselemente und Footer zählen allerdings mit rein, wobei wir bei Google davon ausgehen können, dass der tatsächliche Content extrahiert werden kann. Der folgende Plot zeigt das Verhältnis zwischen Content-Länge und Position:

Wie wir sehen, sehen wir nix, bis auf einen interessanten Ausreißer mit mehr als 140.000 Wörtern in einem Dokument (http://katalog.premio-tuning.de/), der auf Platz 3 für das Keyword “tuning kataloge” rankte. Ansonsten ist keine Korrelation zu beobachten. Eine allgemeingültige Aussage wie “mehr Text = bessere Position” lässt sich somit nicht ableiten. Der Median für die Anzahl Wörter liegt bei 273, der Mean bei 690. Nur zur Erinnerung, wir befinden uns hier in den Top 10. Wie die Kollegen von Backlinko auf 1.890 Wörter für das durchschnittliche 1. Platz-Dokument gekommen sind, würde mich tatsächlich sehr interessieren. Zwar haben sie weit mehr Suchergebnisse angesehen (was bedeutet “1 million search results”? Genau das, also ungefähr 100.000 Suchergebnisseiten, also die Ergebnisse für ungefähr 100.000 Suchanfragen?), aber welchen Durchschnitt sie verwendet haben, verraten sie nicht. Wie man schon in meinen Zahlen sehen kann, gibt es einen großen Unterschied zwischen dem Median und dem Mean, also dem arithmetischen Mittel, das die meisten Menschen als Durchschnitt bezeichnen. Nicht umsonst sage ich immer, dass der Durchschnitt der Feind der Statistik ist Vielleicht sind Texte in den USA aber auch länger? Aber da uns die Zahlen nicht zur Verfügung gestellt werden… und auch nicht die Methoden… nun ja, irgendwann habe ich mal gelernt, dass man zu seinen Ergebnissen sowohl die Daten als auch die Software zur Auswertung beifügen muss, damit wirklich alles nachvollziehbar ist.

In diesem abschließenden Teil habe ich noch weitere Signale hinzugefügt, u.a. TF/IDF und WDF/IDF. Und wie man in der Korrelationsmatrix schön sehen kann, haben wir nirgendwo eine Korrelation. Im letzten Teil hatten wir aber auch schon gesehen, dass das nicht über alle Keywords gilt. In dem Histogramm der Korrelationskoeffizienten sahen wir sowohl positive als auch negative Korrelationen, aber keinen p-Wert. Schaut man sich nur die Korrelationskoeffizienten an, bei denen p < 0.05 ist, sieht das Bild wieder anders aus:

Wir haben also Keywords, wo die Backlinks eine Rolle spielen, und wir haben auch Keywords, wo die anderen Signale eine Rolle spielen. Wenn wir aus dem Keyword-Set eine Schlussfolgerung ziehen können, dann die, dass es keine allgemeingültige Regel gibt. Wie schon beim letzten Teil geäußert, benötigen wir die obige Korrelationsmatrix für jedes Keyword. Und genau das ist spannend, denn wir können für jedes Keyword einzeln oder vielleicht auch ein Thema schauen, wie sich die Ranking-Signale dort verhalten.

Und so sieht man für das Keyword “player update” (als Hash 002849692a74103fa4f867b43ac3b088 in den Daten im Notebook), dass einige Signale doch stärker hervortreten, siehe die Abbildung auf der linken Seite. Kann man nun sicher sein, dass man jetzt für dieses Keyword genau weiß, wie das Ranking funktioniert? Nein, kann man nicht (zumal wir hier noch nicht die p-Werte ausgerechnet haben). Aber wenn wir uns mehrere Keywords aus der gleichen “Region” (also ähnliche Werte in diesem Signal) anschauen, dann könnte tatsächlich etwas darin zu finden sein.
Leider auch nix. Und das war wohl der größte Streitpunkt auf der SEO Campixx. Ich nutze in diesem Beispiel erst einmal nur den Exact Match, also finde ich genau das eingegebene Keyword so im Text. Natürlich könnten wir jetzt weiter gehen und stemmen und auseinander gepflückte Keywords matchen lassen, aber um die Komplexität zu verringern, schauen wir und halt nur den Exact Match an. Schauen wir einmal hier:

Hier ist kein eindeutiges Muster zu sehen, und es gibt auch keine Korrelationen. Nur sehr wenige Beobachtungen schaffen überhaupt einen p-Wert unterhalb 0,05 sowie einen Korrelationskoeffizienten von mehr als 0.1. In diesem Keywordset kann nicht nachvollzogen werden, dass WDF/IDF etwas bringt, zumindest nicht für Exact Match. Ebenso wenig TF/IDF. Keyword Density hab ich nicht mal nachgeschaut.
Der letzte Teil meiner Präsentation von der SEO Campixx war eine Kurzzusammenfassung meiner Artikelserie über ein SEO-Reporting mit R und AWS (insbesondere der Teil über das handlungsrelevante Analysen und ein Reporting).
Noch einmal die wichtigsten Punkte:
Die emotionalen Reaktionen mancher Kollegen sind nicht unverständlich, denn schließlich werden manche Tools teuer bezahlt (es saßen ja auch Tool-Betreiber in meinem Vortrag, von denen einer sich zu der Aussage hinreißen ließ, dass man merke, dass ich lange nicht mehr als SEO gearbeitet hätte). Es ist ungefähr so als ob ich zu einem Christen gehe und sage, dass sein Jesus leider nie existiert hat. Das habe ich nicht gesagt. Ich habe lediglich gesagt, dass ich die Wirkung gängiger Praktiken anhand meines Datensatzes nicht nachvollziehen kann. Aber viele SEOs, die ich sehr schätze, haben mir gesagt, dass z.B. WDF/IDF für sie funktioniere. In der Medizin heißt es “Wer heilt hat Recht”, und am Ende des Tages kommt es auf das Ergebnis an, auch wenn nachgewiesen ist, dass Homöopathie nicht hilft.nUnd vielleicht kommen die guten Resultate dieser SEOs auch nur dadurch zustande, dass sie auch viele andere Dinge richtig machen, es dann aber auf WDF/IDF schieben.
Was mich als Daten-Mensch aber interessiert ist die Reproduzierbarkeit. In welchen Fällen funktioniert WDF/IDF und wann nicht? Hinzufügen möchte ich, dass ich keinerlei kommerzielles Interesse daran habe, irgendeinen Weg als gut oder schlecht zu bezeichnen, denn ich verkaufe kein Tool (mal sehen, vielleicht baue ich ja mal irgendwann eines) und ich verdiene mein Geld nicht mit SEO. Mit anderen Worten: Mir ist es so ziemlich sch***egal, was hier rauskommt. Die Wahrscheinlichkeit, dass ich einem Bestätigungsfehler unterliege, weil ich nur noch Fakten suche, die meine Meinung unterstützen, ist äußerst gering. Mich interessiert nur die Wahrheit in einer post-faktischen Welt. Und anders als zum Beispiel die Untersuchung von Backlinko stelle ich meine Daten und meinen Code zur Verfügung, damit das jeder nachvollziehen kann. Das ist Komplexität, und viele versuchen Komplexität zu vermeiden und suchen einfache Antworten. Aber auf schwierige Fragen gibt es nun mal keine einfachen Antworten, auch wenn das für Menschen viel attraktiver ist. Meine Empfehlung: Keiner Statistik glauben, die nicht die Daten und Methoden nachvollziehbar macht. Ich wünsche mir von allen Kritikern, dass sie auch die Daten und ihre Software offenlegen mögen. Hier geht es nicht um Eitelkeit.
Die Donohue–Levitt-Hypothese ist für mich ein gutes Beispiel: So wurde die Zero Tolerance-Vorgehensweise der New Yorker Polizei in den 90er Jahren dafür gelobt, dass die Kriminalität daraufhin signifikant zurück ging. Das ist bis heute eine weit verbreitete Meinung. Donohue und Levitt hatten die Zahlen untersucht, kamen aber auf eine andere Schlussfolgerung, nämlich dass dies eine Scheinkorrelation sei. In Wirklichkeit sei die Verbreitung der Babypille dafür verantwortlich gewesen, dass die jungen Straftäter erst gar nicht geboren werden, was sich dann in den 90er Jahren bemerkbar machte. Natürlich wurde auch das wieder angegriffen, dann wieder bestätigt, und dann fand auch noch jemand heraus, dass das Verschwinden des Blei-Anteils aus Benzin für die Verringerung der Jugendkriminalität verantwortlich sei (Lead-Crime-Hypothese). Allerdings sind das komplexere Modelle. Mehr Polizeiknüppel gleich weniger Kriminalität ist einfacher zu verstehen und wird deswegen auch immer noch verteidigt (und vielleicht ist ja auch ein bisschen was dran?). Aber auch hier, wer ein Modell sympathischer findet, der wird sich vor allem die Daten anschauen, die diese Meinung bestätigen.
Ich hätte noch viel mehr untersuchen können. Aber wie gesagt, ich mache das nebenbei. Lust auf mehr Daten zu dem Thema habe ich schon. Aber jetzt liegen erst mal wieder andere Datenberge hier Und dann wäre der nächste Schritt ein größerer Datensatz sowie Machine Learning, um Muster genauer zu identifizieren.
Jetzt ist der Vortrag schon wieder einen Monat her, und ich hab immer noch nicht alles runtergeschrieben. Das liegt allerdings auch daran, dass ich die letzten Wochen noch mehr Daten akquiriert habe, damit ich einen Datensatz habe, den ich teilen kann und der nicht kundenspezifisch ist.
80% der Zeit geht für das Validieren und Bereinigen der Daten drauf, so die Faustregel, und ich würde noch einen Punkt hinzufügen, nämlich das Transformieren der Daten. Daten liegen selten so vor, dass man sie gleich verwenden kann.
Aber eines nach dem anderen. Für diesen Teil wollte ich Backlink-Daten sowie Crawl-Daten hinzufügen, nur gibt es die Backlink-Daten bei Google nur noch für die eigene Domain, und wenn man Tools wie Sistrix nutzt, dann kosten die API-Abfragen nun mal Geld bzw. Credits. Am Beispiel von Sistrix erläutert: Für die Abfrage nach Backlinks (links.overview) bezahlt man 25 Credits, mit 50.000 Credits pro Woche kann mal also für 2.000 URLs die Links abfragen. Allerdings kann ich nur die Credits verwenden, die am Ende der Woche nicht für andere Tools verbraten wurden, so dass ich also für 14.099 unique Hosts, die ich im letzten Teil mit den 5.000 Suchanfragen generiert habe, mehr als 7 Wochen benötigen würde. Bis dahin habe ich 1.000 andere Projekte und vergessen, was ich hier an Code geschrieben habe Also habe ich ein Sample genommen auf Basis von 500 Suchanfragen, die ich zufällig aus meinen 5.000 Suchanfragen gezogen habe. Leider war die Ratio unique Hosts/alle URLs hier nicht so schön wie bei dem Gesamtset, 2.597 unique Hosts waren abzufragen.
Dummerweise hatte mir die Sistrix API hier auch noch einen kleinen Strich durch die Rechnung gemacht, denn für über 250 URLs bekam ich Antworten, die mein Skript nicht richtig abgefangen hatte, z.B.
`{“method”:[[“links.overview”]], “answer”:[{“total”:[{“num”:903634.75}], “hosts”:[{“num”:21491.504628108}], “domains”:[{“num”:16439.602383232}], “networks”:[{“num”:5979.5586911669}], “class_c”:[{“num”:9905.3625179945}]}], “credits”:[{“used”:25}]}

Mein Skript hatte Integer-Werte erwartet (Bruchteile eines Backlinks gibt es meiner Meinung nach nicht) und dann einfach gar nix in den Dataframe geschrieben, wenn eine Zahl von Sistrix kam, die kein Integer war. Aber selbst wenn es das abgefangen hätte, die Zahl, die ich hier sehe, hat nichts mit der Zahl zu tun, die ich im Webinterface sehe, wobei es auch hier ab und zu komische Zahlen gibt (siehe Screenshot). Sind das nun 197.520 Backlinks oder 19.752.000? Bitte nicht falsch verstehen, Sistrix ist eines meiner Lieblingstools, aber solche Sachen machen mich wahnsinnig, und R ist da auch nicht ganz einfach Es half nix, ich musste erst mal die Daten durchsehen und zum Teil manuell (!!!) ergänzen. Und wie schwierig R manchmal sein kann, zeigt sich dann, wenn man bestehende Daten ergänzen möchte, aber die vorhandenen Daten in einer Spalte nicht auf NA setzen will. Meine unelegante Lösung der Transformation (die mich 2 Stunden gekostet hat):
test <- merge(sample_2018_04_02,backlinks_2, by = “host”, all.x = TRUE) test <- cbind(test, “backlinks_raw”=with(test, ifelse(is.na(total.y), total.x, total.y))) `
Für das Alter einer Domain hatten wir ja letztes Mal schon gesehen, dass uns Daten fehlen, aber hier existiert ja auch die offizielle Aussage von Google, dass das Alter einer Domain keinen Einfluss auf das Ranking hat. Allerdings waren die alten Domains in der Mehrzahl, so dass man eventuell davon ausgehen könnte, dass neuere Domains geringere Chancen haben, in den Index zu kommen oder in die Top 10, es dann aber egal ist für die jeweilige Position in den Top 10. Die Aussage haben wir aber explizit nicht getroffen, denn es könnte ja sein, dass die fehlenden Alters-Werte in meinem Datensatz genau die jüngeren Domains sind. Das gilt es also noch herauszufinden, allerdings nicht mehr als Teil dieser Serie. Dann könnte ich auch gleich mal die Top 100 untersuchen
Zusammengefasst: Es sieht alles immer ganz einfach aus, aber das Sammeln, Transformieren und Bereinigen der Daten kostet einfach sehr viel Zeit und Energie.

Wir wollen uns zunächst einmal anschauen, ob wir allein durch das Plotten der einzelnen Variablen in Bezug zueinander etwas erkennen können. Die Variablen, die wir hier jetzt haben, sind:
Da fehlen noch ein paar Variablen, aber wir fangen erst einmal hiermit an. Wie wir schön sehen können, sehen wir so gut wie nix Also schauen wir uns noch mal die nackten Zahlen an:

Hier sehen wir schon etwas mehr. Zum Beispiel eine (z.T. sehr schwache) Korrelation zwischen http und backlinks_log, year und backlinks_log, Speed und year, backlinks_raw und ip usw. Aber warum überhaupt die Logarithmisierung der Backlinks? Das wird an dem folgenden Beispiel deutlich:

Schauen wir uns im Histogram die Verteilung der Häufigkeiten der Backlinks an, so sehen wir ganz links einen hohen Balken und ansonsten nicht viel. Kein Wunder, denn in den Suchergebnissen haben wir Hosts wie Youtube, die eine neunstellige Anzahl von Backlinks haben, aber die meisten Hosts haben viel viel weniger Backlinks. Nutzen wir stattdessen einen Logarithmus, also “stauchen” wir das etwas zusammen, dann sieht das Histogram schon ganz anders aus:

Wir sehen hier halt, dass viele Hosts irgendwo in der Mitte sind, einige mit wenigen Links rausstechen (das ist der Balken bei der 0) und wenige Hosts sehr viele Backlinks haben. Spannend ist dann auch die Frage, ob bei jeder Suchanfrage die Anzahl der Backlinks der einzelnen Suchtreffer vergleichbar ist. Die Antwort hier ist nein, wie das folgende Histogram zeigt (auch logarithmisiert):

Ich habe hier für jedes Keyword die durchschnittliche Anzahl der Backlinks berechnet und dann logarithmisiert auf das Histogram gepackt (ohne Logarithmus sähe das Histogram aus wie das unlogarithmisierte davor). Und wie wir schön sehen, haben wir auch hier Bereiche, wo die Suchergebnisse von Hosts kommen, die wenig Backlinks haben, die meisten Suchergebnisse tummeln sich in der Mitte, und bei ganz wenigen Suchergebnissen haben wir eine enorme Anzahl von Backlinks. Dazu muss immer gesagt werden, dass der Durchschnitt keine wirklich tolle Geschichte ist. Aber wir sehen zumindest, dass wir verschiedene “Regionen” haben.
Nachdem wir geklärt haben, warum bestimmte Daten logarithmisiert werden, schauen wir uns jetzt mal genauer an, wie die Korrelationen aussehen, angefangen mit Alter und Backlinks:

Wenn wir ein wenig die Augen zukneifen, dann sehen wir eine Anmutung einer Linie, es sieht fast so aus, als gäbe es eine Korrelation zwischen Alter einer Domain und ihren Backlinks. Einmal getestet:
Pearson’s product-moment correlation
data: dataset$year and dataset$backlinks_log
t = -24.146, df = 4286, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.3721183 -0.3194161
sample estimates:
cor
-0.3460401
Das sieht gut aus. Und es ist auch nicht komplett überraschend. Denn je länger eine Domain existiert, desto mehr Zeit hatte sie, Links zu sammeln. Zwar wissen wir bei einer Korrelation nicht, in welche Richtung sie geht, aber es ist unwahrscheinlich, dass eine Domain älter wird, je mehr Backlinks sie bekommt.
Schauen wir uns das auch noch mal an für die Kombination Alter und Geschwindigkeit:
Pearson’s product-moment correlation
data: dataset$year and dataset$SPEED
t = 13.129, df = 4356, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.1663720 0.2234958
sample estimates:
cor
0.1950994
Interessant ist hier, dass der Korrelationskoeffizient positiv ist, d.h., je älter eine Domain ist, desto langsamer ist sie Womit wir wieder bei den Hygienefaktoren wären.
Gute Frage. Denn wie schon im letzten Teil besprochen gilt das nicht für jedes Keyword. Schauen wir uns mal die Korrelation zwischen Backlinks und Position pro Keyword an und werfen die ausgegebenen Korrelationskoeffizienten dann auf ein Histogram:

Ganz deutlich haben wir hier einige Keywords, deren rankende Hosts eine mindestens schwache wenn nicht sogar moderate Korrelation mit der Anzahl der Backlinks aufweisen. Das heißt, wir müssten also für jedes Keyword einzeln schauen, wie sich das Ranking zusammen setzt. Und da wir eh schon wissen, dass das Ranking dynamisch ist, sehen wir das hier noch etwas klarer.

Leider ist es nicht so, dass ein Zusammenhang zwischen der durchschnittlichen Anzahl von Backlinks der gerankten Seiten sowie der Korrelation zwischen Backlinks der Fundstellen sowie Position gibt. Wir sehen in dem Screenshot auf der linken Seite, dass das sehr bunt gemischt ist.
Woran kann das liegen? Zum Beispiel daran, dass ich hier nur die Daten für die Backlinks für die Hosts habe, nicht für die jeweilige Landing Page. Das wäre natürlich noch schöner, und am idealsten wäre es, wenn ich mir dann noch anschauen könnte, wie die Zusammensetzung der einzelnen Faktoren der Backlinks aussähe. Angesichts meiner Credit-Armut ist das momentan aber nicht möglich. Und hier haben wir wieder ein typisches Problem im Bereich der Data Science: Wir wissen, dass die Daten da draußen sind, aber wir kommen nicht dran. Dennoch bietet diese Vorgehensweise schon enorme Vorteile: Ich kann nämlich jetzt für jedes Keyword einzeln anschauen, wie sich das gegenwärtige Ranking zusammensetzt und dementsprechend agieren. In dem Beispiel links sehe ich, dass ich bei “Datenschutz” viele Backlinks für den Host benötige, in meinem Datensatz (nicht auf dem Screenshot) benötigt mein Host aber wenig Backlinks für Suchanfragen wie “gedichte vorruhestand”. Wir benötigen also für jedes Keyword genau dieses Korrelationsmatrix anstatt einer Gesamtsicht wie oben.
Im [nächsten Teil][10] holen wir uns dann weitere Daten dazu (wir fingen ja mal mit TF/IDF und WDF/IDF an).
[1]: Kommentare (seit Februar 2020 ist die Kommentarfunktion von meinem Blog entfernt):
Steffen Blankenbach says
http://tom.alby.de/wp-content/uploads/2018/04/Bildschirmfoto-2018-04-02-um-12.09.07.png [2]: http://tom.alby.de/wp-content/uploads/2018/04/matrix.png [3]: http://tom.alby.de/wp-content/uploads/2018/04/Bildschirmfoto-2018-04-03-um-01.14.04.png [4]: http://tom.alby.de/wp-content/uploads/2018/04/hist.png [5]: http://tom.alby.de/wp-content/uploads/2018/04/hist_log.png [6]: http://tom.alby.de/wp-content/uploads/2018/04/00000b.png [7]: http://tom.alby.de/wp-content/uploads/2018/04/data-science-seo-age-backlinks.png [8]: http://tom.alby.de/wp-content/uploads/2018/04/plot_zoom_png.png [9]: http://tom.alby.de/wp-content/uploads/2018/04/Bildschirmfoto-2018-04-03-um-02.17.36.png [10]: http://tom.alby.de/data-science-meets-seo-teil-5/
In den ersten beiden Teilen ging es darum, was Data Science überhaupt ist und warum WDF/IDF-Werte sehr wahrscheinlich wenig mit dem zu tun haben, was bei Google unter der Motorhaube passiert. In diesem Teil geht es einen Schritt weiter, wir schauen nämlich, ob es Korrelationen zwischen Ranking Signalen und der Position gibt. Im Vortrag hatte ich das am Beispiel einer Suchanfrage gezeigt und angesichts der zur Verfügung stehenden Zeit auch eher kurz abgehandelt. Hier kann ich in die Tiefe gehen. Wir schauen uns hierbei allerdings erst einmal nur jedes einzelne Rankingsignal in Bezug auf die Positon an, nicht die eventuell vorhandene Wirkung der Rankingsignale untereinander.
Da mein Vortrag bei manchen Kollegen für Schnappatmung und zum Teil “interessante” Äußerungen gesorgt hat, war ein Punkt wahrscheinlich untergegangen. Denn ich hatte ausdrücklich gesagt, und das wiederhole ich hier, dass ich nicht die Aussage treffe, dass man von diesen Daten davon ausgehen kann, dass das Ranking so funktioniert. Wer einmal mit Rechtsanwälten oder Statistikern zu tun hatte weiß, dass diese sich nur ungern auf belastbare Aussagen festnageln lassen wollen. Schließlich kennen wir in der Regel nicht die Gesamtpopulation und müssen daher von einem kleinen Sample auf die Grundgesamtheit schließen; wer ist denn so verrückt und lässt sich darauf festnageln? Daher all die Komplexität mit Konfidenzniveau, Konfidenzintervallen etc…
Die folgenden Aussagen beziehen sich auf ein Sample von 5.000 Suchanfragen. Das klingt nach viel, aber wir wissen nicht, ob diese Suchanfragen der Gesamtpopulation aller Suchanfragen entsprechen. Die Ergebnisse gelten also für das Sample, und ich bin jederzeit bereit, dass für andere Suchanfragen zu wiederholen, wenn mir diese Suchanfragen zur Verfügung gestellt werden.
Weitere Probleme in diesem Ansatz: Wir haben Zugriff auf ein paar Ranking-Signale, aber nicht alle, und die wenigen Signale, die wir haben, sind zum Teil auch noch ungenau. Wir haben von den über 200 Ranking-Signalen:
Uns fehlen also Signale wie
Zusammengefasst haben wir nur einen Bruchteil der Daten, und von denen sind einige auch nicht mal genau. Und meine Berechnungen basieren zudem auf Suchanfragen, von denen wir nicht wissen, ob sie repräsentativ sind.
Mein Lieblingsbeispiel für den verhängnisvollen Glauben an Korrelationen ist der statistische Zusammenhang zwischen den Marktanteilen des Microsoft Internet Explorers und der Mordrate in den USA zwischen 2006 und 2011. Zwar mag es witzig sein zu behaupten, dass hier ein Zusammenhang besteht (und das führt auch regelmäßig zu einem Lacher in Vorträgen), aber Tatsache ist, dass hier ein statistischer Zusammenhang, den wir als Korrelation bezeichnen, kein wirklicher Zusammenhang sein muss. Korrelation bedeutet nicht Ursache und Wirkung. Schlimmer noch, in der Statistik wissen wir nicht mal, in welche Richtung der statistische Zusammenhang läuft. In diesem Beispiel also, ob die Marktanteile des Internet Explorers zu mehr Morden geführt haben, oder ob die Morde dazu geführt haben, dass man danach den Internet Explorer benutzt hat, um seine Spuren zu verwischen.
Natürlich sind die Zusammenhänge in manchen Situationen klar: Wenn ich mehr Geld ausgebe bei AdWords, dann bekomme ich evtl. mehr Conversions. Und wenn wir den statistischen Zusammenhang zwischen Ranking-Signalen untersuchen, dann ist es wahrscheinlich, dass mehr Backlinks zu einer besseren Position führen, auch wenn natürlich eine bessere Position dafür sorgen kann, dass mehr Webseitenbetreiber interessante Inhalte finden und diese verlinken… Wir wissen aber nicht, ob zum Beispiel die einzelnen Signale sich untereinander beeinflussen können, und wir schauen uns in der Regel ja auch nur die Top 10 an. Wie im vorherigen Teil beschrieben ist das eine Art Jurassic Park, wo wir nicht das ganze Bild haben.
Jede Analyse beginnt mit einer Beschreibung der Daten. Für die 5.000 Suchanfragen haben wir mehr als 50.000 Suchergebnisse bekommen, aber die Ergebnisse, die auf Google-Dienste zeigen, nehmen wir erst einmal raus, da wir nicht wissen, ob diese nach den normalen Ranking-Faktoren gerankt werden. Es bleiben 48.837 URLs über, die sich auf 14.099 Hosts verteilen.
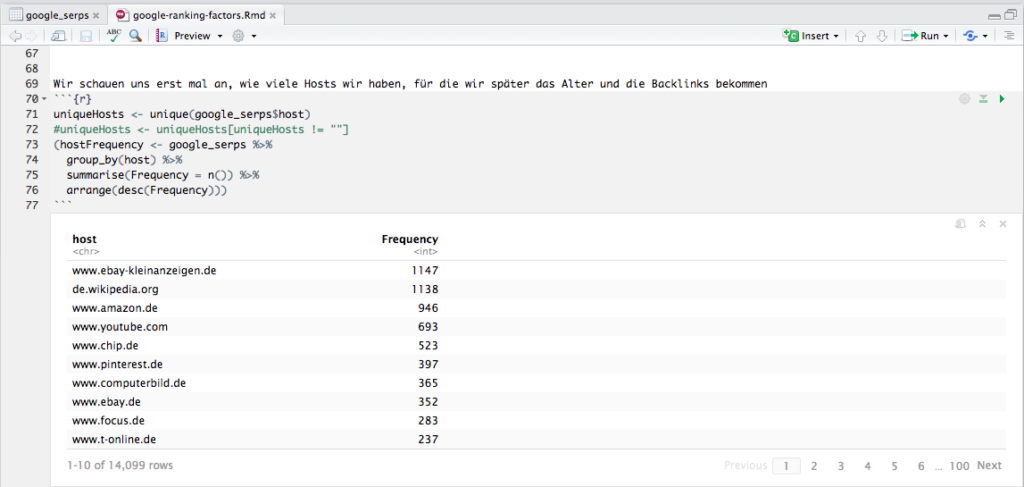
In letzter Zeit arbeite ich vermehrt mit dplyr, das ein Piping ermöglicht wie unter Linux/UNIX; diese Funktionalität wurde dem magrittr-Package entliehen, und sie macht den Code unglaublich übersichtlich. In dem Beispiel in der Abbildung werfe ich nach der auskommentierten Zeile meinen Dataframe google_serps auf group_by(), das nach host gruppiert, und das Ergebnis dieses Schritts werfe ich auf summarise(), das mir dann die Häufigkeiten pro Host berechnet, und das werfe ich zum Schluß noch auf arrange(), was das Ergebnis absteigend sortiert. Das Ergebnis schreibe ich in hostFrequency, und weil ich das Ergebnis in meinem R Notebook sofort sehen will, setze ich den ganzen Ausdruck in Klammern, damit das Ergebnis nicht nur in den Dataframe hostFrequency geschrieben wird, sondern auch gleich ausgegeben. Jedes Mal, wenn ich sowas mit dplyr mache, freue ich mich einen Ast. Und wenn man richtig große Datensätze hat, dann macht man das gleiche mit sparklyr :).
Aber zurück zum Thema: Wir sehen hier also, dass wenige Hosts sehr häufig ranken, und das heißt umgekehrt, dass viele Hosts nur einmal ranken. Keine Überraschung hier.
Die Speed-Daten für jeden Host sind sehr einfach zu bekommen, denn Google bietet dafür die PageSpeed Insights API an, und netterweise gibt es hierfür auch ein R Package. Bei über 10.000 Hosts dauert die Abfrage etwas, und mehr als 25.000 Anfragen pro Tag darf man nicht stellen sowie nicht mehr als 100 (?) Anfragen pro 100 Sekunden. Ich hab das einfach laufen lassen, und nach 1 Tag war mein R abgestürzt und alle Daten verloren. Nicht schön, aber ein Workaround: Nach jedem Request den Dataframe auf die Festplatte schreiben.
Aber schauen wir uns die Daten jetzt einmal genauer an. Hier ist ein Histogramm der Verteilung der Speed-Werte von 14.008 Hosts (ich hab also für 99,4% der Hosts einen PageSpeed-Wert erhalten):

Wir sehen, dass die meisten Hosts es über die 50 Punkte schaffen, und summary gibt uns folgende Zahlen:
Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00 55.00 70.00 66.69 82.00 100.00
Schön ist hier zu sehen, wie irreführend der Durchschnitt sein kann Und nun plotten wir einmal Positionen versus Speed:

Wie wir sehen, sehen wir nix. Das prüfen wir noch einmal genauer:
cor.test(google_serps$position,google_serps$SPEED) Pearson’s product-moment correlation data: google_serps$position and google_serps$SPEED t = -5.6294, df = 48675, p-value = 1.818e-08 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.03438350 -0.01662789 sample estimates: cor -0.02550771
Sieht so aus als ob es keine Korrelation zwischen PageSpeed und Position in den Top 10 gäbe (wir wissen nicht, ob es vielleicht eine gäbe in den Top 100, könnte ja sein, dass die Plätze 11 bis 100 schlechtere PageSpeed-Werte haben). Aber es ist auch nicht unwahrscheinlich, dass wir es mit einem Hygiene-Faktor zu tun haben: Wenn man gut rankt, dann hat man keinen Vorteil, wenn man schlecht rankt, dann wird man bestraft. Das ist ungefähr so als ob man duscht, dann merkt es keiner, aber wenn man nicht geduscht hat, dann fällt es auf. Oder, kurz gefasst (so soll ich es auf der SEO Campixx gesagt haben), eine langsame Webseite ist wie nicht geduscht zu haben Allerdings sehen wir auch Hosts, die trotz einer gruseligen Speed ranken. Aber wenn man nach “ganter schuhe” sucht, dann ist http://ganter-shoes.com/de-at/ wohl das beste Ergebnis, auch wenn die Seite bei mir 30 Sekunden zum Laden benötigt.
Bedenken sollten wir auch, dass die PageSpeed API eine Echtzeit-Messung durchführt… vielleicht haben wir nur einen schlechten Moment erwischt? Man müsste eigentlich mehrmals die PageSpeed messen und daraus einen Durchschnitt erstellen.
Was wir auch sehr einfach bekommen an Daten, ist die Unterscheidung, ob ein Host https verwendet oder nicht. Während manche die Verwendung sicherer Protokolle als einen gewichtigen Rankingfaktor ansehen, sehen gemäßigtere Stimmen wie Sistrix die Verwendung von SSL eher als schwachen Rankingfaktor. In diesem Datensatz haben 70% aller URLs ein https. Aber bedeutet das auch, dass diese Seiten besser ranken?
Wir haben es hier mit einer besonderen Form der Berechnung zu tun, denn wir versuchen den Zusammenhang zwischen einer kontinuierlichen Variable (der Position) und einer dichotomen Variable (SSL ja/nein) zu ermitteln. Die beiden Varianten des Protokolls wandeln wir um in Zahlen, http wird zu einer 0, https zu einer 1 (siehe Screenshot unten in den Spalten secure und secure2).
Die Ermittlung des Point-Biserial Koeffizienten ist ein Sonderfall des Pearson Korrelation Koeffizients; normalerweise würden wir in R einfach cor.test(x,y) eingeben, aber hierfür wird ein zusätzliches Paket geladen, was diese Sonderform unterstützt. Tatsächlich unterscheiden sich die Werte der beiden Tests aber kaum, und cor.test liefert mir zudem noch den p-Wert.

Wie wir sehen, sehen wir nix oder fast nix: Mit einem Korrelations-Koeffizienten von -0,045067 können wir ausschließen, dass https einen Einfluss auf das Ranking in den Top 10 gehabt hat. Bedeutet das, dass wir alle wieder auf https verzichten sollten? Nein, denn für den Nutzer ist es besser. Und sobald Browser noch deutlicher zeigen, dass eine Verbindung nicht sicher ist, werden sich die Nutzer eher schneller von einer Seite verabschieden. Ganz abgesehen davon, dass wir uns hier ja nur die Top 10 angesehen haben. Es könnte ja sein, dass die Plätze 11 bis 1000 vor allem von Seiten ohne SSL belegt waren. Und dann könnten die Ergebnisse schon wieder anders aussehen.
Vielleicht haben wir es bei SSL als Ranking-Faktor aber auch mit einem umgekehrten Hygienefaktor zu tun. Google hätte zwar gerne SSL, aber da manche wichtige Seite evtl noch kejn SSL hat, verzichtet man darauf. So wie man vielleicht gerne hätte, dass der Traumpartner geduscht ist, aber wenn die oder der dann plötzlich vor einem steht, dann ist es doch egal, weil man halt so verliebt ist. Auf Dauer geht das natürlich nicht gut. Und so wird das bei SSL auch sein
Gehen wir zu dem nächsten Ranking-Signal, dem Alter einer Domain, auch wenn es heißt, dass das Alter einer Domain keine Rolle spielt. Hier stehen wir vor einer ersten Herausforderung: Wie bekomme ich möglichst automatisch und vor allem zuverlässig das Alter einer Domain heraus? Sistrix bietet das Alter einer Domain an, aber nicht die eines Hosts (der Unterschied wird im Skript zu meinem SEO-Seminar an der HAW erklärt). Trotzdem hat Sistrix den Vorteil, dass die API sehr schlank und schnell ist. Allerdings findet Sistrix für 2.912 der Domains (nicht Hosts) kein Alter, bei 13.226 unique Domains sind das dann 22% ohne Domain-Alter. Jurassic Park lässt grüßen (wer diese Anspielung nicht versteht, bitte den zweiten Teil über Data Science und SEO lesen). Schauen wir uns dennoch einmal die Verteilung an:

Wir sehen eine leicht rechtsschiefe Verteilung, d.h. dass wir links bei den älteren Domains eine höhere Frequenz sehen (nein, ich sehe nicht spiegelverkehrt, so bezeichnet man das halt). Jüngere Domains scheinen hier geringere Chancen zu haben. Allerdings kann es auch sein, dass Sistrix gerade jüngere Domains nicht in der Datenbank hat und die knapp 3.000 fehlenden Domains eher rechts anzusiedeln wären.
Können wir wenigstens hier eine Korrelation sehen? Wir plotten die Daten erst einmal:
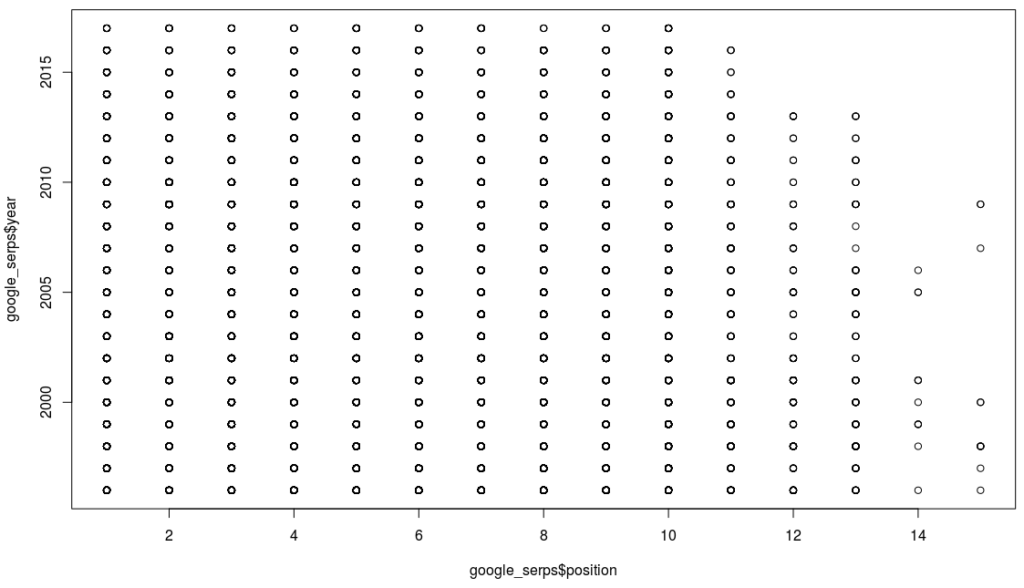
Auch hier sehen wir nix, und wenn wir uns die Korrelation berechnen lassen, dann bestätigt sich das:
cor.test(google_serps$position,as.numeric(google_serps$year)) Pearson’s product-moment correlation data: google_serps$position and as.numeric(google_serps$year) t = 1.1235, df = 44386, p-value = 0.2612 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.003970486 0.014634746 sample estimates: cor 0.005332591
Ich habe nicht nur keine Korrelation, sondern liege auch außerhalb des Konfidenzniveaus. Das Ergebnis ist aber mit viel Vorsicht zu genießen, denn wie oben schon erwähnt kann es sein, dass unsere Auswahl einfach nicht repräsentativ ist, denn vermutlich wird nicht jede Domain die gleiche Chance gehabt haben in die Domain-Alter-Datenbank von Sistrix zu kommen. Wir müssten diese Daten also ergänzen und eventuell auch die Daten von Sistrix überprüfen (ich habe nicht herausfinden können, woher Sistrix die Daten hat); leider habe ich auch kein Muster identifizieren können, denn manchmal zeigt die eine Quelle ältere Daten an, manchmal eine andere Quelle. Im Prinzip müsste man alle Datenquellen nehmen und dann immer das älteste Datum nehmen. Nur leider lassen sich die meisten Quellen auch nicht so einfach scrapen Und somit haben wir nicht nur fehlende, sondern auch zum Teil fehlerhafte Daten. Und das ist kein untypisches Problem im Data Science Bereich.
Da ich schon bald die 2.000 Wörter zusammen habe (und ich die Korrelation Wörter/”bis zum Ende des Artikels gelesen” für mein Blog kenne), werde ich die nächsten Ranking-Faktoren im nächsten Blogpost begutachten. Wichtig: Wir sehen hier zwar, dass wir für angeblich sehr wichtige Ranking-Faktoren keine Evidenz finden, dass sie tatsächlich einen Einfluss haben. Aber das bedeutet nicht, dass das wirklich stimmt:
Beispiel:
cor.test(google_serps$position[google_serps$keyword==“akne vitamin a”],google_serps$secure2[google_serps$keyword==“akne vitamin a”]) Pearon’s product-moment correlation data: google_serps$position[google_serps$keyword == “akne vitamin a”] and google_serps$secure2[google_serps$keyword == “akne vitamin a”] t = -4.6188, df = 8, p-value = 0.001713 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.9645284 -0.4819678 sample estimates: cor -0.8528029
Auch wenn das Konfidenzintervall hier sehr groß ist, es bewegt sich für diese Suchanfrage “akne vitamin a” immer noch im Bereich einer mittleren bis starken Korrelation (es korreliert negativ, weil die Positionen von 1 bis 10 oder weiter hoch gehen). Es gilt also auch die Segmente oder “Regionen” zu identifizieren, wo bestimmte Signale eine Wirkung haben. Dazu mehr im nächsten Teil über Data Science und SEO.